Noise Floor Dbm Hz

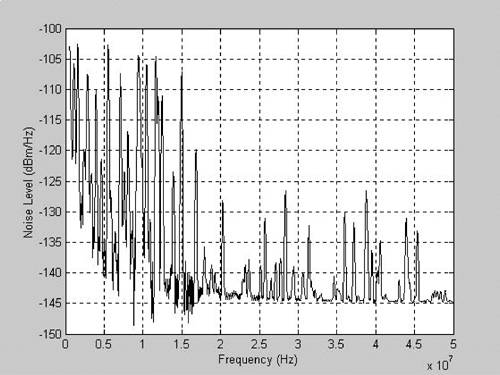
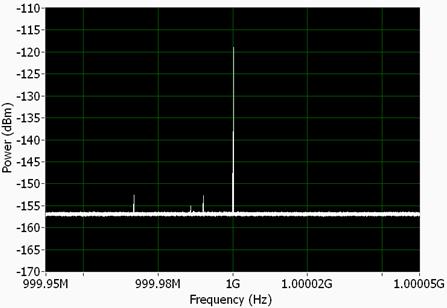
When i wanted to compare the noise of the real circuit which i built the spectrum analyzer could only display in dbm.

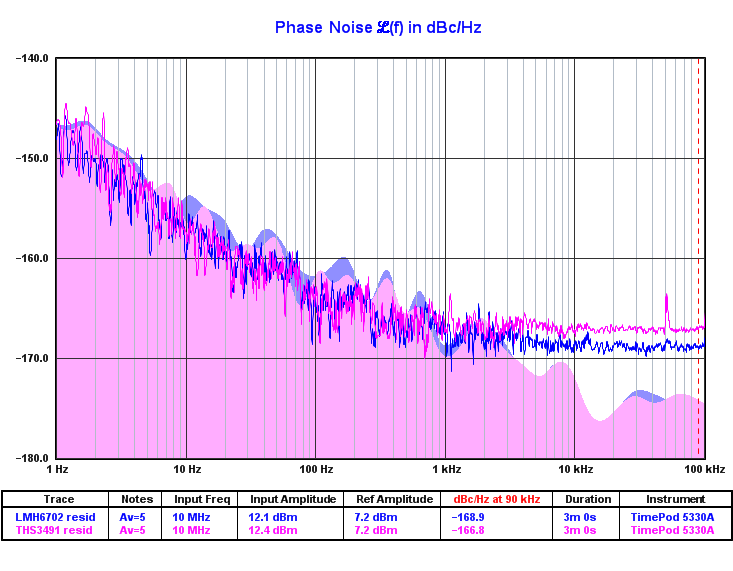
Noise floor dbm hz. Relative to the bandwidth we can use the reference level of 174 dbm hz and simply multiply it by the actual bandwidth of the radio channel. Since the units of ktb are watts hz calculate the noise floor in the channel bandwidth by multiplying the noise power in a 1 hz bandwidth by the overall equivalent noise bandwidth in hz. Johnson nyquist noise thermal noise johnson noise or nyquist noise is the electronic noise generated by the thermal agitation of the charge carriers usually the electrons inside an electrical conductor at equilibrium which happens regardless of any applied voltage thermal noise is present in all electrical circuits and in sensitive electronic equipment such as radio receivers can. For a receiver with a 10 khz enbw we calculate the noise floor in db milliwatts dbm as follows.

Spice will produce a plot of the power density given in v sqrt hz. 0 dbm is 1 mw. Of course small changes in power occur as the unknown noise is far below the known and. 1 hz noise floor equates to a noise power of 174 dbm so a 1 khz bandwidth would generate 174 10 log 10 1 khz 144dbm of noise power the noise is thermal noise johnson noise.

Actual noise source power is at the original noise floor level. P is the power in watts k is boltzmann s constant 1 38 x 10 23 j k b is the bandwidth in hertz. Because the power level is proportional to the bandwidth twice the bandwidth level gives twice the power level 3db and ten times the bandwidth gives ten times the power level 10db. This relationship allows you to calculate the noise power of signals below the measurement noise floor.

Mds 10log kto 1e3 nf 10log bw snr. It is then easy to relate this to other bandwidths. Thermal noise in a 50 ω system at room temperature is 174 dbm hz. Using this formula it is possible to determine that the minimum equivalent input noise for a receiver at room temperature 290 k is 174 dbm hz.