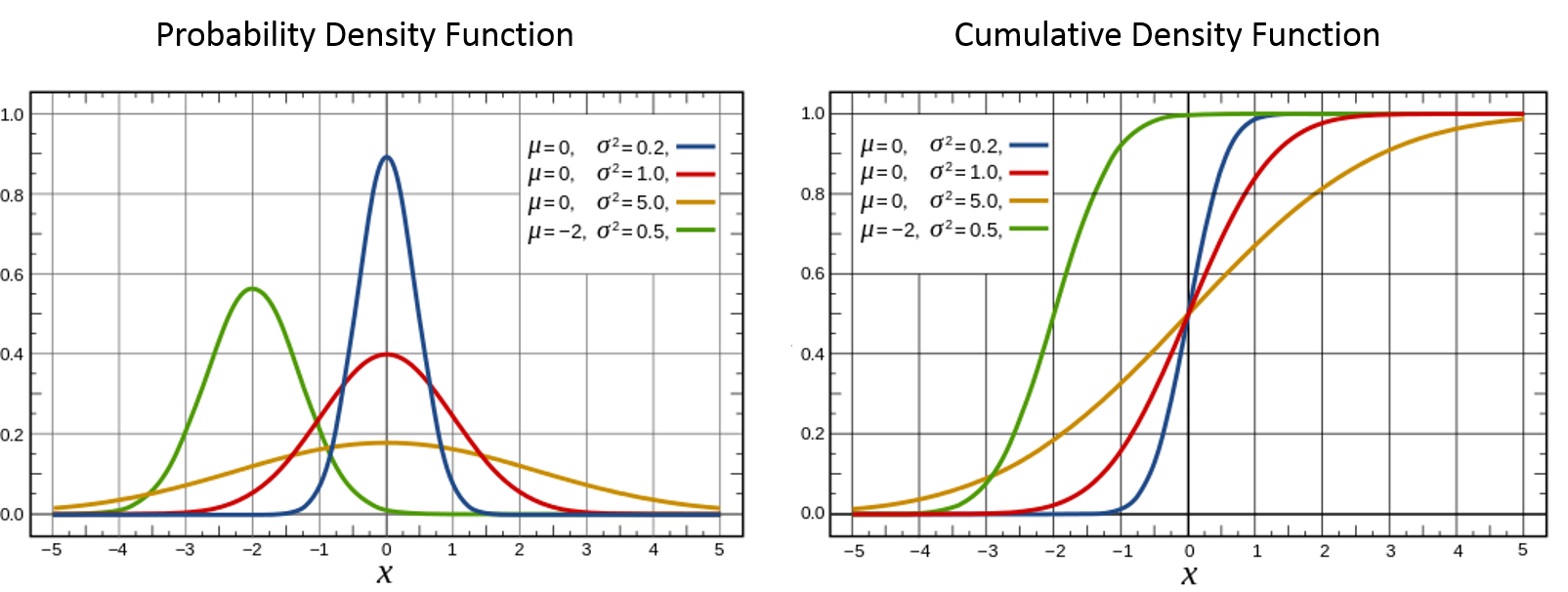
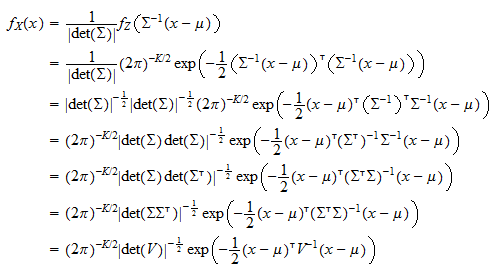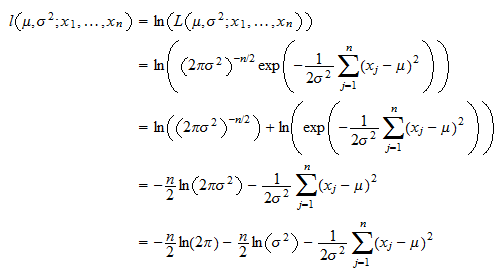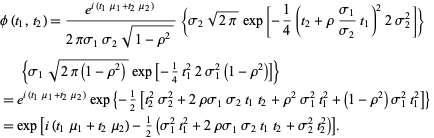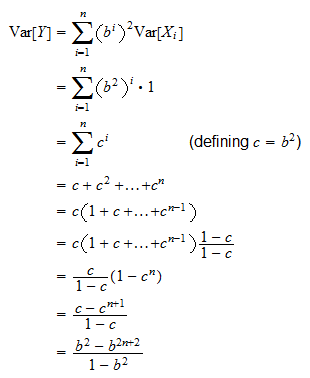Normal Distribution Matrix Form

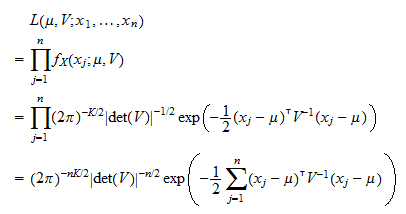
We have the following form for the density function.

Normal distribution matrix form. Do october 10 2008 a vector valued random variable x x1 xn t is said to have a multivariate normal or gaussian distribution with mean µ rn and covariance matrix σ sn 1. We will assume for now that σ is also positive definite but later on we will have occasion to relax that constraint. The maximum likelihood estimation mle of the parameters of the matrix normal distribution is considered. By marco taboga phd.

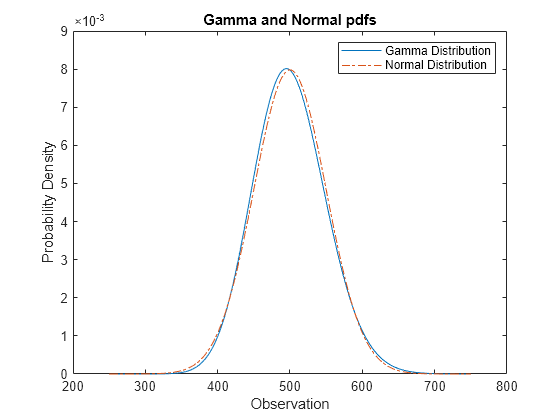
This lecture presents some important results about quadratic forms involving normal random vectors that is about forms of the kind where is a multivariate normal random vector is a matrix and denotes transposition. The circularly symmetric version of the complex normal distribution has a slightly different form. 60e99 one of the most important probability distributions. 2010 mathematics subject classification.

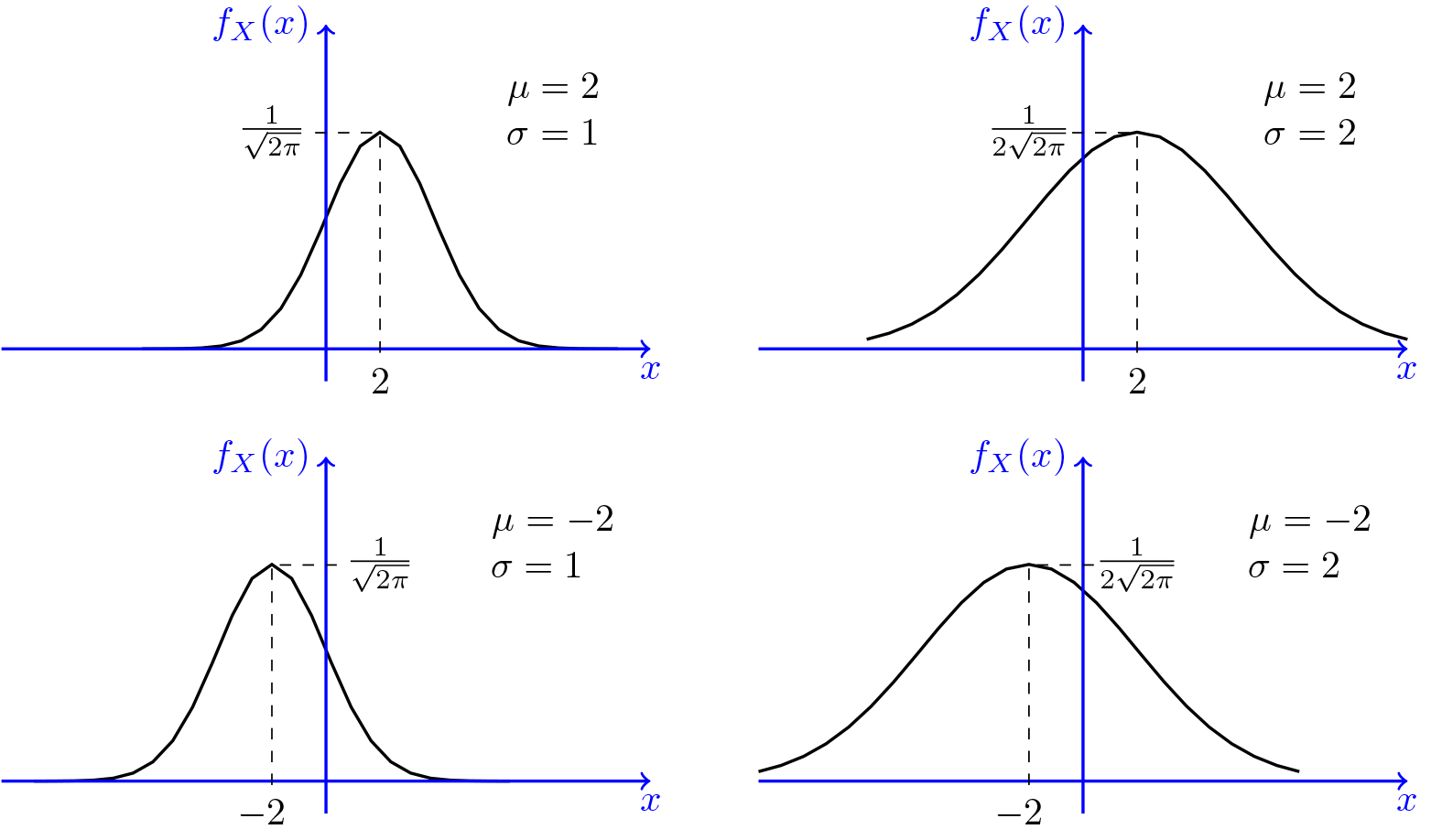
Each iso density locus the locus of points in k dimensional space each of which gives the. A single real number. Normal distribution quadratic forms. Where is a real k dimensional column vector and is the determinant of the equation above reduces to that of the univariate normal distribution if is a matrix i e.

By marco taboga phd. The multivariate normal mv n distribution is a multivariate generalization of the one dimensional normal distribution in its simplest form which is called the standard mv n distribution it describes the joint distribution of a random vector whose entries are mutually independent univariate normal random variables all having zero. The product term given by captial pi π acts very much like the summation sign but instead of adding we multiply over the elements ranging from j 1 to j p inside this product is the familiar univariate normal distribution where the random variables are subscripted by j in this case the elements of the random vector mathbf x 1 mathbf x 2 cdots. The multivariate gaussian distribution is commonly expressed in terms of the parameters µ and σ where µ is an n 1 vector and σ is an n n symmetric matrix.

In the absence of analytical solutions of the system of likelihood equations for the among row and among column covariance matrices a two stage algorithm must be solved to obtain their maximum likelihood estimators. In statistics the matrix normal distribution or matrix gaussian distribution is a probability distribution that is a generalization of the multivariate normal distribution to matrix valued random variables. The most common form of standard normal distribution table that you see is a table similar to the one below click image to enlarge. The multivariate gaussian distribution chuong b.

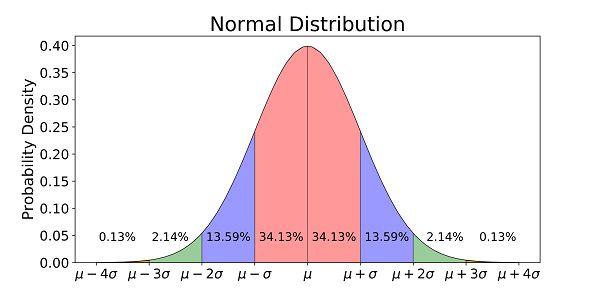
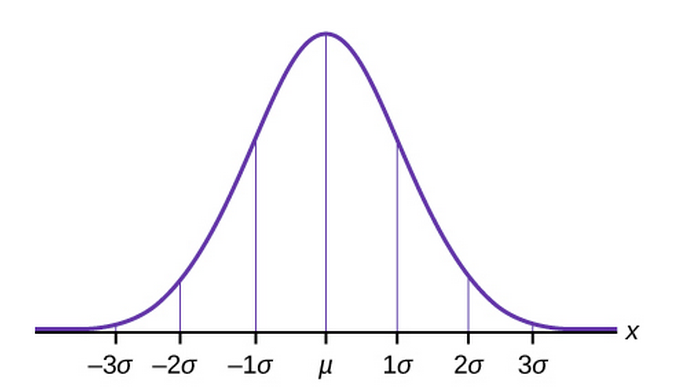
The term normal distribution is due to k. Pearson earlier names are gauss law and gauss laplace distribution it is used both in relation to probability distributions of random variables cf.